1. 题面

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

示例 1：

输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作，
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。
示例 2：

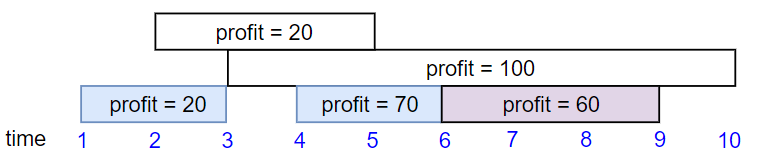
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。
共获得报酬 150 = 20 + 70 + 60。
示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

提示：

1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-profit-in-job-scheduling
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.题目分析

区间调度问题

题目给出了一个startTimes[i]和endTimes[i],这两个数组规定了一个区间，如果是简单的区间调度问题，那么我们只需要使用扫描线的模板将区间给它合并起来就可以。

最优解

但是现在题目引入了profits[i]这个量，要求在合并区间的基础上，同时要能够获得最大的得分

是否可以贪心?

一个想法是，在合并区间的时候，由于区间的合并的基础单位是两个区间，因此在选择区间进行合并的时候，合并的时候选择收益更大的区间就能够获得更大的收益。

但是其实这种想法是错误的，因为我们发现贪心选择的过程并不是互相独立的，而是依赖于上一次选择的结果。为什么这样说，我们从理论上分析，对于三个区间叠在一起的情况下，这时候合并区间的时候有C32种选择，而后的合并结果都与这次合并有关。举个例子来进行分析:

这里的话我们改一下上面的图，我们profit[A] = 50,profit[B] =20,profit[C] = 30，这个例子就能够说明为什么不能够进行贪心了，首先注意到A和B是重叠的，因此要合并取优，因此合并完成之后(将A和B进行合并)，合并之后发现A和B形成大区间与C重叠，这时候又要进行合并，A和B形成的大区间profit[A+B] = 70,而profit[C] = 30，这时候合并ABC，也就是profit[A+B+C] = 70。这个结果显然是错误的，因为我们完全可以将B不进行合并，因为A和C不重叠，因此可以直接选profit[A+B] = 50+30=80，这才是最优解。

穷举

通过上面的分析，我们发现本次合并状态与上一次选择的结果有关，而且我们需要进行所有状态的穷举才能够得到一个正确答案。

那么提到了这几个关键词，很明显，就应该要上动态规划了。

3. 动态规划思路

状态分析

状态就是在检索第i个兼职工作的时候，能够获得的报酬。

选择分析

情况1:如果A和B的工作时间重叠了，那么我可选的报酬有选A获得的报酬和选B获得的报酬，还有A和B都不选获得的报酬

情况2:如果A和B的工作时间不重叠，那么我可选的报酬就是A和B的报酬都选上。

dp数组定义

根据状态而言，假设我们已经求出了[0...i-1]兼职工作所能得到的最大报酬，那么在选择第i份兼职工作的时候，肯定是在之前[0...i-1]能够得到的最大兼职工作报酬的基础上再选一份兼职工作得到的。

因此可以这样定义dp[i]:在前i个兼职工作中选择兼职工作，能够获得的最大报酬。

状态转移方程

状态转移方程主要依据于dp数组和选择

base-case

dp[0] = 0:前0个兼职工作也就是没有工作，也就是报酬是0

dp[n]:前n个兼职工作也就是选遍了所有的兼职工作的最大报酬

int[] dp = new int[n+1];
dp[0] = 0;
...
return dp[n];

状态如何转移?

状态的转移依赖于选择

如果我们不选择第i个工作，那么最大的报酬就等于前i-1个工作的最大报酬。
如果我们选择第i个工作，由于工作时间不能够重叠，那么我所选择的上一个区间的最大工作报酬不能够和第i个工作所重叠。怎么样是不重叠的标志呢?当上一个区间的结束时间比本区间的开始时间还要早的话，那么就证明肯定不会重合，而且题目还说如果刚好结束，那么结束的那一刻开始就可以直接开始下一份工作。
设j是满足endTime[j]<=startTime[i]的j，写出状态转移代码如下

for(int i = 1;i<=n;i++){
    for(int j  = i-1;j >= 0;j--){
        if(endTime[j]<=startTime[i-1]){
            //注意下标的转换问题,由于dp数组的定义,i所对应的worktimes要改一下
            //j对应的是原数组的下标,但是在dp数组的定义又不同,也要改一下
            pre = j+1;
            break;
        }
        //做出你的选择
        dp[i] = Math.max(dp[i-1],dp[pre]+works[i-1].profit);
    }
}

至此，这道题的核心就全部分析完毕了，然后就是编码验证。

4. 编码

public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
    //将startTime和endTime合并为一个区间
    List<int[]> inteval = new ArrayList<>();
    //这里的话可以先填充一个占位符进去
    inteval.add(new int[]{-1,-1,-1});
    //接着就是将数组存进去
    int n = startTime.length;
    for(int i = 0;i<n;i++){
        inteval.add(new int[]{startTime[i],endTime[i],profit[i]});
    }
    //对区间进行排序,按照结束时间
    Collections.sort(inteval, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            return o1[1]-o2[1];
        }
    });
    //然后开始遍历该区间
    int[] dp = new int[n+1];
    dp[0] = 0;
    for(int i = 1;i<=n;i++){
        //然后就是找到一个合适的区域
        int target = inteval.get(i)[0];
        int pre=0;
        for(int j =i-1;j>=1;j--){
            if(inteval.get(j)[1] <= target){//结束时间早于开始时间
                pre = j;
                break;
            }
        }
        dp[i] = Math.max(dp[i-1],dp[pre]+inteval.get(i)[2]);
        System.out.println(dp[i]+" "+pre);
    }
    return dp[n];
}

提交之后发现是可以通过的，但是时间复杂度很高，n方的复杂度，这里的话有一个优化思路，将查找上一个的这个过程做成二分查找，因为数组是有序的，优化后循环外层是n的复杂度，内层是logn的复杂度，提升为nlogn的复杂度。

public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
    //将startTime和endTime合并为一个区间
    List<int[]> inteval = new ArrayList<>();
    //这里的话可以先填充一个占位符进去
    inteval.add(new int[]{-1,-1,-1});
    //接着就是将数组存进去
    int n = startTime.length;
    for(int i = 0;i<n;i++){
        inteval.add(new int[]{startTime[i],endTime[i],profit[i]});
    }
    //对区间进行排序,按照结束时间
    Collections.sort(inteval, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            return o1[1]-o2[1];
        }
    });
    //然后开始遍历该区间
    int[] dp = new int[n+1];
    dp[0] = 0;
    for(int i = 1;i<=n;i++){
        //然后就是找到一个合适的区域
        int target = inteval.get(i)[0];
        int pre=getIndex(inteval,target,i)-1;
        dp[i] = Math.max(dp[i-1],dp[pre]+inteval.get(i)[2]);
        System.out.println(dp[i]+" "+pre);
    }
    return dp[n];
}

private int getIndex(List<int[]> intervals,int target,int end){
    int left = 1,right = end;
    //定义搜索区间为[left,right)
    //需要寻找的是右侧边界
    while (left<right){//结束条件是left==right,因此最终返回left或者right都可以
        int mid = left+(right-left)/2;
        int midNum = intervals.get(mid)[1];
        if(midNum == target){
            //寻找右侧边界,左侧边界向右边逼近
            left = mid+1;
        }else if(midNum > target){
            //已经检查过了mid,而mid是比target要大的
            right = mid;
        }else if(midNum < target){
            //已经检查过了mid,而mid是比target要小的,因此left
            left = mid+1;
        }
    }
    return left;
}